8.1   Geometría

8.1.1 Objetivos:

• Relacionar la ecuación algebraica de cada  sección cónica con su representación geométrica.
• Definir apropiadamente como un conjunto de puntos las diferentes secciones cónicas, en especial la circunferencia, la elipse  y la hipérbola.
• Dadas las ecuaciones respectivas de las secciones cónicas determinar en cada una de ellas sus respectivas gráficas y sus puntos principales.

8.1.2  Introducción

Hemos visto en capítulos anteriores las funciones cuadráticas de la forma         f(x) = ax² + bx + c y  las formas de desarrollarlas mediante diversos procedimientos y nos hemos dado cuenta que pertenecen a la clase  de relaciones llamadas parábolas.

Hay una clase  de relaciones más amplia denominada secciones cónicas que pueden ser descritas como secciones transversales formadas por la intersección de un cono con un plano. Estas relaciones que incluyen la circunferencia, la hipérbola y  la elipse son las que se estudiarán en la presente unidad.

8.2   Secciones cónicas

8.2.1   Sección cónica: Se puede definir como la intersección de un cono con las diferentes posiciones de un plano, o como sitios geométricos de puntos que cumplen propiedades geométricas específicas.

8.2.2   La circunferencia

Una de las definiciones más comunes de circunferencia se enuncia como un lugar geométrico de los puntos de un plano que están a la misma distancia de un punto fijo llamado centro.

La distancia a la cual se hace referencia se llama radio de la circunferencia.

Consideremos la siguiente circunferencia con centro en el punto (0,0) y radio  r, con la particularidad de que el radio debe ser mayor que cero.  r > 0.

De la figura tomemos el punto  P₁ = (x₁, y₁) siendo este un punto cualquiera que esté sobre  la circunferencia. La distancia que hay entre el centro (0, 0) y el punto P₁ es la que llamamos radio de la circunferencia.

La distancia entre dos puntos cualesquiera está dada por la fórmula:

x² + y² = r²

Siendo esta la fórmula general de la circunferencia con centro en el origen

La anterior fórmula se puede enunciar de la siguiente manera:

toda ecuación de la forma   x² + y² = r² donde r es un número positivo > 0, representa una circunferencia con centro en el origen (0, 0) del sistema de coordenadas y radio r. Con las siguientes características:

• Es una ecuación de segundo grado en las variables  x  y  y.
• Los coeficientes de   x² y y² son iguales.
• El radio de la circunferencia equivale a la raíz cuadrada del término independiente.

Entonces:

8.2.2.1   Ecuación de la circunferencia con centro en un punto diferente al  origen.

Ahora veamos  que sucede cuando la circunferencia tiene el centro en cualquier punto diferente al origen.

Sea la figura:  

La gráfica corresponde a una circunferencia con centro  c (h, k) y radio  r > 0.

para el caso particular de la circunferencia con centro diferente al origen se tiene que:

De los anteriores procedimientos se desprende la ecuación general de la circunferencia, que viene dada por:                          

Ejemplos:

1. Dar la ecuación de la circunferencia con centro  C(-2, 4) y radio 4 cm.

Como el centro no está en el origen del plano cartesiano, la ecuación corresponde a la forma:

                                             (x – h) ² + (y – k)² = r²   

Reemplazando los valores conocidos:             [x – (-2)]² + (y – 4)²   = 4²

Eliminando paréntesis:                                        (x + 2) ² + (y – 4)²  = 4²

Resolviendo los cuadrados:                     x² + 4x + 4 + y² –8y + 16 = 16

Ordenando e igualando a cero:                       x² + y² + 4x – 8y + 4 =  0

Por lo tanto la ecuación pedida es:                 x² + y² + 4x – 8y + 4 = 0

Por Completación de cuadrados en los dos paréntesis, es decir sumando a cada paréntesis el cuadrado de la mitad del coeficiente de x y de y , se tiene:                    

3. Hallar la ecuación de la circunferencia que pasa por los puntos (4, 3) y (-2, -5). En un plano cartesiano se ubican los puntos dados, y se traza una circunferencia de tal forma que la circunferencia pase por encima de los puntos, como se muestra en la figura.

Se observa que para hallar el centro de la circunferencia se debe encontrar el punto medio del segmento comprendido entre los puntos  (-2, -5)  y  (4, 3).

Para desarrollar este ejercicio es necesario hacer algunas precisiones.

De la demostración de este teorema nos ocuparemos en capítulos posteriores, por el momento apliquemos estos valores a los puntos dados para hallar el punto medio del segmento comprendido entre los puntos  (-2, -5)  y  (4, 3), que para nuestro caso como se ve en la figura es el mismo centro de la circunferencia.

Entonces se tiene:

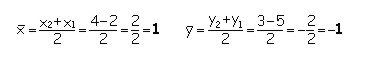El punto medio del segmento será:  P_m = (1, -1) que a su vez es el centro de la circunferencia. Para hallar el valor del radio de la circunferencia basta aplicar la fórmula de distancia entre el centro de la circunferencia y uno de los puntos que pasan por encima de la circunferencia,  luego entonces:

Tomemos el punto (4, 3) y el centro de la circunferencia (1, -1)

r² = (x – h)² + (y – k)² 

r² = (4 – 1)² + (3 +1)²

r² = (3)² + (4)²

r² = 9 + 16

r² = 25   

Ahora, como la circunferencia  no tiene el centro en el origen, es de la forma:

r² = (x – h)² + (y – k)²

La ecuación buscada será:         (x – 1)² + (y + 1)² = 25

8.2.3   La elipse

La elipse es el conjunto de todos los puntos del plano, tales que la suma de las distancias a dos puntos fijos llamados focos es constante.

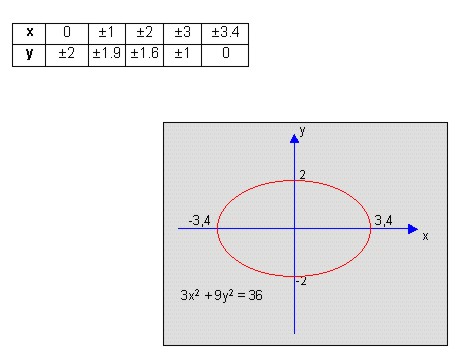
Toda ecuación de la forma   ax² + by² = k  con a, b, k como términos que se conocen y de igual signo, representan una elipse.

Ejemplo:

Representar gráficamente la ecuación   3x² + 9y² = 36

Como se ha hecho en casos anteriores, despejamos el valor de la incógnita  y, para asignarle valores independientes a la variable  x y así poder hallar los valores respectivos de y.

Ecuación dada:     3x² + 9y² = 36

Tabulando se tiene:

Como se puede observar, la figura obtenida es una elipse con las siguientes características:

• Es una ecuación de segundo grado en las variables  x  y  y.
• Los coeficientes de   x² y y² son del mismo signo.

8.2.4   La hipérbola

Una hipérbola es el conjunto de puntos (x, y) de tal manera que la diferencia de sus distancias a dos puntos fijos llamados focos es constante.

Toda ecuación de la forma  ax² - by² = k  donde a puede ser igual a b, representa una hipérbola, con las siguientes características:

• Es una ecuación de segundo grado en las variables  x  y  y.
• Los coeficientes de   x² y y² son de signo contrario, aunque en valor absoluto pueden ser iguales.

Ecuación dada:         y² - 3x² = 6

8.3 Geometría del espacio                                                     

La diferencia con la geometría plana o de dos dimensiones que estudia las figuras cuyas partes están todas en un mismo plano, la geometría del espacio o de tres dimensiones trata de las propiedades de las figuras cuyas partes no están todas en un mismo plano.

Se denomina plano a toda superficie indefinida que contiene totalmente cualquier recta que pasa por dos de sus puntos.

El plano suele representarse por un paralelogramo y está determinado por:

1. Una recta y un punto exterior a ella

Por una recta puede pasar un plano. Haciendo girar este plano alrededor de la recta, se llega el momento en que alcanzará el punto, pero si continúa la rotación, dejará de contenerlo. Luego por la recta y el punto solo puede pasar un plano.

2. Por tres puntos no situados en una misma recta

Se sabe que dos puntos determinan la posición de una recta, este caso se reduce al caso anterior.

3. Por dos rectas que se cortan

Un punto de cada una de las rectas y el de su intersección determinan un plano, según hemos explicado anteriormente, por otra parte, este plano contiene cada una de las rectas puesto que contiene dos de sus puntos.

4.  Por dos rectas paralelas

Dos rectas paralelas están por definición en un mismo plano, y cualquier otro plano que las contenga, se confunde con el primero ya que pasa por una de las paralelas y por un punto de la otra.

8.3.1   Sólidos regulares                                                        

Son los sólidos o poliedros que poseen tres dimensiones y a los cuales se les puede determinar: Área lateral (A _L)_, Área total (A_t), y volumen (V).

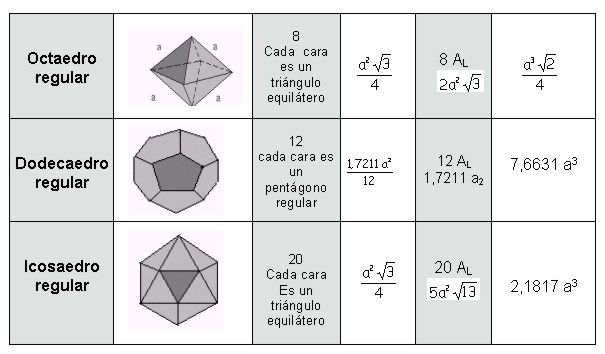
Existen cinco sólidos regulares con 4, 6, 8, 12 y 20 caras respectivamente cuyas características se pueden observar en el siguiente cuadro:

8.3.1.1   Aplicaciones

1. Hallar el área lateral de un tetraedro regular de arista igual a 6 cm.

Como las caras de un tetraedro regular son triángulos equiláteros, el área lateral será uno de los triángulos, luego entonces:

Arista  a = 6 cm.

2. La arista de un hexaedro regular es de 10 cm. ¿Cuál será el valor  del volumen?

Arista  a = 10 cm.

Volumen = a³

V = (10 cm)³

V = 1000 cm³.

8.3.2   Poliedros                                                                

Un poliedro es un cuerpo o sólido geométrico limitado por planos. Las intersecciones de estos planos forman polígonos llamados  caras del poliedro, los lados de las caras se llaman aristas , y las intersecciones de las aristas reciben el nombre de vértices.

La Diagonal  de un poliedro es toda recta que une dos vértices no situados en una misma cara.

Un poliedro es convexo cuando está situado en su totalidad en un mismo lado de cada una de sus caras.

De la anterior definición se puede concluir que:

• Todo plano secante a un poliedro convexo, lo corta un polígono convexo.
• Una recta no puede cortar un poliedro convexo de más de dos puntos.

8.3.2.1 Poliedro regular  

Es aquel cuyas caras son polígonos regulares iguales y cuyos ángulos poliedros son también iguales. Según el número de sus caras los poliedros se clasifican en tetraedros, pentaedros. Hexaedros, etc., según tengan cuatro, cinco, seis, etc. Caras.

8.3.3   Prismas

Se llama prisma al poliedro que tiene dos caras iguales y paralelas y las demás caras son paralelogramos.

Las caras iguales y paralelas se llaman bases, y las demás caras laterales. La intersección de cada par de caras laterales consecutivas recibe el nombre de arista lateral.

La altura de un prisma es la distancia que hay entre las dos bases, y se mide por la perpendicular común a ellas.

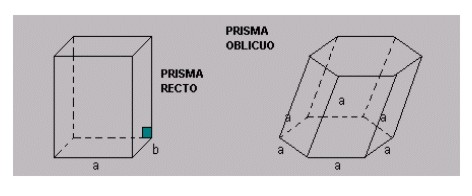
Un prisma es recto u oblicuo según que sus aristas laterales sean perpendiculares u oblicuas a las bases. En el prisma recto, las aristas laterales son iguales a la altura, y en el prisma oblicuo son mayores que ella.

Un prisma es triangular, cuadrangular, pentagonal, etc. si sus bases son triángulos, cuadriláteros, pentágonos, etc.

8.3.3.1   Prisma regular. Es un prisma recto cuyas bases son polígonos regulares.

8.3.3.2  Sección recta de un prisma es la sección determinada por un plano perpendicular a las aristas laterales.

8.3.3.3  Tronco de prisma es la parte de prisma comprendida entre una de las bases y un plano oblicuo a ella que corta todas las aristas laterales.

8.3.3.4  Área del prisma.  Cuando nos referimos al área de la superficie de un cuerpo geométrico suele emplearse  tan sólo la palabra área, para estos casos se sobreentenderá la expresión completa: área de la superficie de los cuerpos geométricos.

El área de un prisma puede ser lateral o total.

8.3.3.5   Área lateral del prisma: el área lateral del prisma es igual al producto de la arista lateral ( altura del prisma) por el perímetro de la sección recta (perímetro de la base), y viene dada por la fórmula:       A _L = P_B h

8.3.3.6   Área total del prisma:  el área total del prisma es igual  al área lateral más la de las bases y se determina por la fórmula:  A _T = P_B h + 2B

8.3.3.7   Volumen del prisma: se llama volumen de un cuerpo geométrico a la medida del espacio que ocupa. El volumen de un prisma cualquiera es igual al producto del área de su base por la altura:         V = Bh

Ejemplo:

Hallar el área lateral, total y volumen de un prisma cuadrilátero regular recto si se sabe que el lado de la base mide 10 cm y su arista lateral 20 cm.

Se halla el valor del área lateral.   A _L = P_B h, donde la altura es la misma arista lateral porque se trata de un prisma recto, es decir  h =20 cm.

El perímetro de la base, como es un prisma cuadrilátero ( cuatro lados iguales) será:         

P_B = 10 cm x 4 = 40 cm

Luego entonces el área lateral del prisma será:

A _L = P_B h   = 40 cm x 20 cm = 800 cm².

Ahora para calcular el área total del prisma, A _T = P_B h + 2B  se halla primero el área de una de las bases. Como el prisma es regular, la base es un cuadrado y por tanto se tiene:  

B = l²  es decir     B = (10 cm)² = 100 cm²

Se halla el valor del área total:

A _T = P_B h + 2B = 800 cm² + 2 (100 cm²) = 1 000 cm²

Finalmente se calcula el volumen del prisma:

V = Bh  = 100 cm² x 20 cm = 2 000 cm³

8.3.4   Pirámides                                                      

Se llama pirámide al poliedro que tiene por base un polígono cualquiera, y por caras laterales tres o más triángulos que tienen un vértice común. Este vértice común es el vértice de la pirámide que también recibe el nombre de cúspide.

Los lados de las caras laterales que concurren al vértice se denominan  aristas laterales.

La altura de una pirámide es la perpendicular trazada desde el vértice a la base

de la pirámide.

Una pirámide es triangular, cuadrangular, pentagonal, etc. si sus bases son triángulos, cuadriláteros, pentágonos, etc.

La pirámide triangular es un tetraedro. Como todas sus caras son triángulos, cualquiera de ellas puede tomarse como base.

8.3.4.1   Pirámide regular

La pirámide regular es aquella que tiene por base un polígono regular cuyo centro coincide con el pie de la altura. En una pirámide regular todas las aristas laterales son iguales porque se apartan igualmente del pie de la altura, y las caras laterales son triángulos isósceles iguales.

Apotema de una pirámide regular es la altura de los triángulos que forman las caras laterales.

8.3.4.2  Área lateral: el área lateral de la pirámide es igual a la suma de  las áreas de las caras laterales. Se tiene que al desarmar una pirámide triangular se obtienen tantos triángulos isósceles como lados tenga la base del sólido. Suele suceder que los triángulos que conforman la pirámide tienen diferentes medidas pero la altura siempre es igual, y se representa por  h.

Como el área lateral de la pirámide es igual a la suma de  las áreas de las caras laterales se tiene:

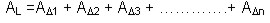Como el área de un triángulo se halla mediante la fórmula:

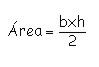Entonces se tiene:

8.3.4.3  Área total: el área total de la pirámide viene dada por el área lateral más el área de la base.

Ejemplo:

Hallar el área total y el volumen de una pirámide cuadrilátera regular recta, sí el lado de la base mide 8 cm y la altura 5 cm.

Como la pirámide es cuadrilátera se tiene:

P_B = 8 cm + 8 cm + 8 cm + 8 cm = 32 cm.

Para calcular la  apotema se debe utilizar el teorema de Pitágoras  en el triángulo rectángulo formado por la altura (5 cm) y la mitad del lado de la base como uno de los catetos, es decir 4 cm.

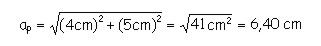Luego entonces:

8.3.4.5   Pirámide truncada

Es la parte de pirámide comprendida entre la base y un plano que corta todas las aristas laterales.

La pirámide truncada tiene las siguientes características:

• Las caras laterales son trapecios.
• La apotema del tronco es la altura de cualquiera de las caras laterales.
• La altura de la pirámide truncada es la perpendicular que une las bases de la misma.

8.3.4.5.1   Área lateral: el  área lateral de una pirámide truncada está definida como el producto de la apotema de la pirámide por la suma de los semiperímetros de la base superior e inferior, y viene dada  por la fórmula:                                             

                                               A _L = ( P₁ + P_s) a_p

Donde:

P₁ = semiperímetro de la base inferior.

P_s = semiperímetro de la base superior.

8.3.4.5.2   Área total: teniendo como base el procedimiento para hallar el área total de los sólidos anteriores, el área total de la pirámide  truncada es la suma del área lateral con las áreas de las bases.

Entonces:   A_T = A_L + B_i + B_S

                     A_T = ( P₁ + P_S) a_p + B_i + B_S

B₁ representa el área de la base inferior, mientras que  B_s representa el área de la base superior.

8.3.4.5.3   Volumen de la pirámide truncada: El volumen de un tronco de pirámide que tenga bases paralelas esta  definido como el producto de la suma de las áreas de las bases, mas la media geométrica de ellas, multiplicadas por un tercio de su altura, y esta representado por la fórmula:                         

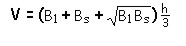Ejemplo:

¿Cuál es el valor para el área total de un tronco de pirámide en la cual la base inferior tiene de ancho 12 cm, el ancho de la base superior es de 8 cm, siendo la altura de la pirámide de 14 cm?

para el desarrollo de este problema se conoce:

Lado de la base inferior = 12 cm.

Lado de la base superior = 8 cm.

Se halla  el área lateral:

8.3.5   Sólidos de revolución                                 

Los sólidos de revolución son los llamados también cuerpos geométricos redondos que se originan cuando un segmento de línea o curva gira sobre un punto llamado eje. La línea que al girar da origen al sólido recibe el nombre de generatriz.

8.3.5.1   Superficie cilíndrica y cilindro:  una superficie cilíndrica es la que esta generada por una recta que se mueve en el espacio, permaneciendo siempre paralela a una recta fija, y recorre una curva también fija.

Como hemos dicho la recta que se mueve se llama generatriz, y la curva fija, directriz.

8.3.5.2   Cilindro                                                    

Es un cuerpo o sólido geométrico limitado por una superficie cilíndrica y dos planos paralelos, llamados bases que cortan todas las generatrices, y tiene infinito numero de caras laterales.

El cilindro  puede ser recto u oblicuo, según que la generatriz sea perpendicular u oblicua a las bases.

Ejemplo:

En un cilindro recto, la generatriz mide 15 cm y el radio de la base  7 cm. Hallar el área lateral, el área total y el volumen del cilindro.

Por el enunciado del problema se tiene:

Generatriz = 15 cm.

Radio de la base =7 cm.

8.3.5.4   Superficie cónica y cono

8.3.5.4.1   Superficie cónica:  Es la que genera una recta llamada generatriz que se mueve en el espacio, girando sobre un punto fijo llamado vértice, y resbala sobre una curva fija denominada directriz.

8.3.5.4.2  Cono

Es un cuerpo o sólido geométrico limitado por uno de los mantos de una superficie cónica y por un plano llamado base, que corta todas las generatrices, y que tiene un número infinito de caras laterales. En este cuerpo geométrico se puede destacar que:

• La base del cuerpo es un círculo.
• En los conos rectos, la altura, el radio de la base y la generatriz forman un triángulo rectángulo.

8.3.5.4.3  Área lateral del cono recto

Ahora, como en el caso anterior, se pueden obtener las fórmulas para hallar el área total y el volumen de un cono recto, que serían:

Ejemplo:

Hallar el volumen de un cono recto de generatriz igual a 10 cm y radio de la base igual a 8 cm.

Para hallar el volumen se utiliza la fórmula:  

Se puede observar que para aplicar  esta fórmula se debe hallar primero el valor de la altura del cono, y la calculamos utilizando el Teorema de Pitágoras en el triángulo rectángulo que  se forma  con el radio y la generatriz del cono como cateto e hipotenusa respectivamente.

Se calcula el volumen:  

8.3.5.4.4  Tronco de cono recto

Es el sólido o cuerpo geométrico que se forma cuando un cono es interceptado por un plano paralelo a la base.

Las fórmulas  para el área lateral, área total y volumen del tronco de cono recto se calculan teniendo como base y desarrollando similar procedimiento al empleado para el cálculo de las fórmulas  del tronco de pirámide recto.

Estas fórmulas serán:

8.3.5.5   Superficie esférica y esfera

8.3.5.5.1  Superficie esférica

Es la que está generada por una semicircunferencia que gira alrededor de su diámetro. Dicho de otra manera sería el lugar geométrico de los puntos del espacio que equidistan de un punto fijo llamado centro.

8.3.5.5.2  Esfera

Es el sólido o cuerpo geométrico generado por un semicírculo que gira alrededor de su diámetro y que está limitado por una superficie esférica.

• Radio: el radio de una superficie esférica o de una esfera, es la recta que une el centro con un punto cualquiera de la superficie esférica.
• Diámetro: es la recta que pasa por el centro de la superficie esférica o de la esfera y une dos puntos de la superficie.
• Plano diametral: es todo plano que pasa por el centro de la esfera. Este plano divide la esfera en dos partes iguales llamados hemisferios.

Todos los radios de una esfera son iguales al igual que los diámetros.

8.3.5.5.3  Círculos de la esfera

Los círculos de la esfera son dos, a saber:

• Círculo máximo. El círculo máximo de una esfera es aquel cuyo plano pasa  por el centro de la esfera, se llama también círculo diametral.
• Círculo menor. Es aquel cuyo plano no pasa por el centro de la esfera.

La deducción de las fórmulas para obtener el área y el volumen de la esfera, compete a capítulos más avanzados de geometría y matemáticas que se tratarán en cursos y unidades  posteriores. Por el momento y para darles aplicación se enuncian:

Ejemplo:

Hallar el área y el volumen de una esfera de 10 cm de diámetro.

Ahora aplicando las fórmulas para el área y el volumen de la esfera: