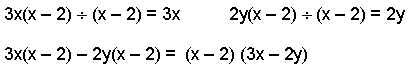5.1  Descomposición factorial

5.1.1  Factor: se llaman factores de una expresión algebraica a las expresiones que multiplicadas entre sí dan como resultado la expresión inicial.

Si multiplico    x  por x + y se obtiene

x ( x + y) = x² + xy  es decir x  y  x+ y  son factores de  x ² + xy

5.1.2  factorizar: es convertir una expresión algebraica  en el  producto indicado de sus factores.

5.2  Casos de factorización    

Para factorizar monomios y polinomios  se utilizan varios procedimientos que se desarrollan mediante situaciones o casos que se presentan con un método particular para cada uno.

5.2.1  Caso I

5.2.1.1 Factor común monomio: se presenta cuando todos los términos de un polinomio tienen  una parte en común, bien sea numérica,  literal o ambas.

Descomponer o factorar la expresión:   a³ – a²x + ax²

los tres términos tienen el factor común a.

Escribimos el factor común  a   como coeficiente de los resultados de dividir cada uno de  los términos  entre el factor común. Estos resultados se encierran dentro de un paréntesis, separados por sus correspondientes signos.

Factor común  a.

a ³  a =  a²      -a²x  a = - ax        ax²  a = x² 

Luego tendremos:   a³ – a²x + ax² =  a (a² – ax + x²)

Ejemplos:  Factorizar

5.2.1.2 Factor común polinomio:                

Factorizar:   3x(x – 2) – 2y(x – 2)

Los dos términos de esta expresión tienen en común el binomio (x – 2),  entonces escribimos el binomio (x – 2) como coeficiente de un paréntesis donde irán los resultados de dividir cada uno de los términos entre el factor común   (x – 2) separados por el signo correspondiente.

        Factor común: (x – 2)  luego:

Se escribe primero el factor común.

Todo caso de factorización se prueba multiplicando los factores obtenidos y comprobando que resulte la expresión algebraica inicial.

5.2.2  Caso II.     Factor común por agrupación

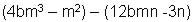El segundo paréntesis va precedido del signo menos -, que corresponde al signo del tercer término, y se sabe que se debe cambiar de signo al término  3n  porque el paréntesis va precedido del signo menos -.

5.2.3  Caso III. Trinomio cuadrado perfecto

Una cantidad es cuadrado perfecto cuando resulta de  un producto de dos factores iguales:

Sí se multiplica   6a x 6a = 36a²  decimos que  36a ² es cuadrado perfecto. De igual manera se dice que  (-6a) x( –6a) = 36a², es decir que –6a es  también la raíz cuadrada de 36a². De lo anterior se concluye que la raíz cuadrada de una cantidad positiva posee dos signos, uno positivo y otro negativo.

Raíz cuadrada de un monomio

Sea el monomio: 16b⁴c⁸ la raíz cuadrada  será   4b²c⁴ 

Porque si multiplicamos   (4b² c⁴) x (4b²c⁴) = 16b⁴c⁸.

Hemos visto que los productos notables pueden ser de dos formas para cuadrados perfectos:

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b² 

Dado el trinomio:  36 + 12m² + m⁴  veamos si cumple las características para ser un trinomio cuadrado perfecto:

Primer término:  36  raíz cuadrada = 6

Tercer término:  m⁴  raíz cuadrada = m²

Doble producto de las raíces cuadradas = 2(6)(m²) =12m²  que debe  corresponder al segundo término del trinomio.

Se puede afirmar que la expresión   36 + 12m² + m⁴ es trinomio cuadrado  perfecto.

Veamos    36 + 12m² + m⁴  = (6+m ²)²  porque:

(6+m²)²  =  (6)² +2(6)(m²) +(m²)²  =  36 + 12m² + m⁴ 

El anterior procedimiento se enuncia mediante la siguiente regla:

Un trinomio ordenado es cuadrado perfecto si el primer y tercer término son cuadrados perfectos, es decir que tiene raíz cuadrada exacta, son positivos y el segundo término es dos veces el producto de sus raíces cuadradas. El segundo término puede ser positivo o negativo.

Ejemplo.

Factorizar:         4x² – 12xy + 9y²

Extraemos las raíces cuadradas del primer y tercer términos:

4x²  raíz cuadrada = 2x

9y²  raíz cuadrada = 3y

doble producto de las raíces cuadradas = 2(2x)(3y)  =  12xy

Luego el resultado será las raíces cuadradas separadas por el signo del segundo término y elevadas al cuadrado o multiplicadas por sí mismos.

Entonces:   4x² – 12xy + 9y²  =  (2x – 3y)²   o   (2x – 3y) (2x – 3y)

Hay  ocasiones en que el primero o tercer o ambos términos de un trinomio  resultan ser expresiones compuestas, y si bien es un caso especial, para su desarrollo se procede de igual manera a lo visto en el ejemplo anterior:

Ejemplo:

Factorizar      (m + n)² – 2(m + n) (a – m) + (a – m)²   

Primer término:     (m + n)²    raíz cuadrada   (m + n)

Segundo término:  (a – m)²   raíz cuadrada   (a – m)

doble producto de las raíces  =  2(m + n) (a – m)

entonces:   (m + n)² – 2(m + n) (a – m) + (a – m)²  = [(m + n) – (a –m)]²

                             = [ m + n – a +m]²

                             = (2m + n – a)²

5.2.4  Caso IV.  Diferencia de cuadrados perfectos

Se ha visto en los productos notables   que la diferencia de los cuadrados de dos cantidades, es igual al producto de la suma por la diferencia  de las raíces cuadradas de las cantidades.

Recordemos:  a² - b² = (a + b) (a - b)

Para factorizar una diferencia de cuadrados  le extraemos la raíz cuadrada tanto al minuendo como al sustraendo y el resultado será el producto de la suma por la diferencia  de las  raíces cuadradas extraídas.

Ejemplos:

Factorizar

1. a² – 25

raíz cuadrada de  a²  =  a

raíz cuadrada de  25 =  5

entonces:  a² – 25  =  (a + 5) (a – 5)

2. 100 – x² y⁶

raíz cuadrada de   100  =  10

raíz cuadrada de  x² y⁶ =  x y ³

entonces:  100 – x² y⁶ = (10 + x y³) (10 - x y³)

 

Al igual que en el caso anterior (caso III) se  pueden encontrar expresiones algebraicas en que en una diferencia de cuadrados uno o ambos cuadrados resultan ser expresiones compuestas. Para el desarrollo de estos casos veamos los siguientes ejemplos.

Factorizar:

1. (x + 1)² – 4x²

raíz cuadrada de  (x + 1)²  = (x + 1)

raíz cuadrada de  4x²  =  2x

entonces   (x + 1)² – 4x²  = [(x + 1) + 2x] [(x + 1) - 2x]

                                       = [x + 1 + 2x] [x + 1 - 2x]

                                       = (3x + 1) (1 – x)

2. m⁶ - (m² - 1)² 

raíz cuadrada de  m⁶ =  m³    

raíz cuadrada de  (m² - 1)² =  (m² - 1)

entonces:   m⁶ - (m² - 1)²  =  [m³ + (m² - 1)] [m³ - (m² - 1)]

                                        = (m ³ + m² - 1) (m³ - m² + 1)

5.2.4.1  Combinación de los casos III  y IV     

Factorizar:

1. a² – b² – 2bc – c²     

El término 2bc indica la existencia de un trinomio cuadrado perfecto, cuyo primer término sería  b²   y su tercer término  c². Luego agrupando de la siguiente manera:

                          = (a +  b + c) (a - b - c)

5.2.5  Caso V.  Trinomio cuadrado perfecto por adición  y sustracción

Es  común encontrar expresiones algebraicas como   4a⁴ + 8a² b² + 9b⁴

Raíz cuadrada de 4a⁴  =  2a² 

Raíz cuadrada de 9b⁴  =  3b²

Doble producto de las raíces  2(2a²) (3b² )  = 12a² b²

Por definiciones y propiedades vistas anteriormente nos damos cuenta que la expresión   4a⁴ + 8a² b² + 9b⁴  no es un trinomio cuadrado perfecto. Pero se puede hacer que esta expresión lo sea, para lo cual se necesita que el segundo término  8a ² b²  se convierta en  12a² b²,  sumándole  4a² b²  y para que el trinomio inicial no se altere se le resta la misma cantidad que se ha sumado. Es decir:

4a⁴ + 8a² b² + 9b⁴ + 4a² b²  - 4a² b²

Sumando términos semejantes:   4a⁴ + 12a² b² + 9b⁴ - 4a² b²

Factorizando el trinomio cuadrado perfecto:  (2a² + 3b²)² - 4a² b²

Factorizando la diferencia de cuadrados:

=  [(2a² + 3b²) + 2ab] [(2a² + 3b²) - 2ab]

=  (2a² + 3b² + 2ab) (2a² + 3b² - 2ab)  ordenando los polinomios:

= (2a² + 2ab + 3b²) (2a² - 2ab + 3b²)

Ejemplo:

Factorizar    36x⁴ – 109x² y² + 49y⁴

Raíz cuadrada de 36x⁴  =  6x² 

Raíz cuadrada de 49y⁴  =  7y²

Doble producto de las raíces  2(6x² ) (7y²)  = 84x² y²

Para que el segundo término del trinomio inicial sea igual a  84x ² y²  se debe sumar 25 x² y², así  -109 x² y² + 25x² y² =  84x² y²  logrando conformar un trinomio cuadrado perfecto, y para que  el trinomio inicial no se altere, restamos la misma cantidad que se ha sumado, luego entonces se tendrá:

36x⁴ – 109x² y² + 49y⁴   =  36x⁴ – 109x² y² + 49y⁴ + 25x² y² - 25x² y²

sumando términos semejantes:

=  (36x⁴ – 84x² y² + 49y⁴) - 25x² y²

Factorizando el trinomio cuadrado perfecto:

= (6x² – 7y²)²  - 25x² y²

Factorizando la diferencia de cuadrados:

= [(6x² – 7y²) + 5xy] [(6x² – 7y²) - 5xy]

despejando paréntesis y ordenando los polinomios:

= (6x² + 5xy – 7y²) (6x² - 5xy – 7y²)

5.2.5.1  Caso especial.  Factorizar una suma de cuadrados

Factorizar:    4m⁴ + 81n⁴

Raíz cuadrada de  4m⁴  =  2m²

Raíz cuadrada de  81n⁴ =  9n²

Para que esta expresión algebraica sea un trinomio cuadrado perfecto hace falta que su segundo término sea igual al Doble producto de las raíces cuadradas 2 (2m²) (9n²)  = 36m² n². Entonces sumamos esta cantidad al trinomio inicial para convertirlo en trinomio cuadrado perfecto y para que éste no se altere se le resta la misma cantidad que se ha sumado. Es decir:

4m⁴ + 81n⁴ + 36m² n² - 36m² n²

se ordena el trinomio cuadrado perfecto y  se factoriza:

(4m⁴ + 36m² n² + 81n⁴)- 36m² n²  =  (2m² + 9n² )² - 36m² n²

Factorizando la diferencia de cuadrados:

= [(2m² + 9n²) + 6mn] [(2m² + 9n²) - 6mn]

despejando los paréntesis y ordenando los polinomios:

= (2m² + 6mn + 9n²) (2m² - 6mn + 9n²)

5.2.6  Caso VI.  Trinomio de la forma    x²   bx  c

De acuerdo a la expresión general son trinomios como   m² -12m + 11,  a² + 7a – 60, y que tienen las siguientes características:

a) El coeficiente del primer término es igual a 1.

b) El primer término es una parte literal cualquiera elevada al cuadrado, es decir es cuadrado perfecto.

c) El segundo término tiene la misma parte literal que el primer término con exponente 1 y coeficiente cualquier número positivo o negativo.

d) El tercer término es un número cualquiera positivo o negativo e independiente del primero y segundo términos.

Ejemplo.

Factorizar:   x² + 3x - 10

Se descompone el trinomio en dos binomios, donde el primer término de cada binomio va a ser la raíz cuadrada del primer término del trinomio:

(x      ) (x     )

En el primer binomio se escribe el signo del  segundo término del trinomio, y en el segundo binomio escribimos el producto del signo del segundo término del trinomio por el signo del tercer término del trinomio:

(x +      ) (x -     )

Ahora se buscan dos números cuya suma sea igual al coeficiente de segundo término del trinomio con su signo correspondiente y cuyo producto sea igual al tercer término del trinomio con su signo correspondiente. Para hallar estos dos números de una forma más rápida se realiza mediante la descomposición del tercer término del trinomio en sus factores primos:

Se han buscado dos números cuya suma algebraica sea igual a 3 y cuyo producto sea igual a – 10. Entonces se concluye que:

x² + 3x - 10 = (x + 5) (x - 2)

Estos trinomios se diferencian de los anteriores (caso VI) en que el primer término tiene un coeficiente diferente de 1. Por tal razón pueden no ser cuadrados perfectos éstos coeficientes.

Ejemplo.

Factorizar:     6x²  + 7x  + 2

El coeficiente del primer término  (6), no es cuadrado perfecto. Para lograr esto multiplicamos todo el trinomio por esta cantidad:

Como inicialmente se multiplicó el trinomio por 6, se debe dividir el trinomio entre la misma cantidad para que no se altere:

5.2.8  Caso VIII. Cubo perfecto de binomios

En los productos notables vimos que:

(a + b)³ = a³ + 3a²b   + 3ab²  + b³

(a - b)³ = a³ - 3a²b   + 3ab²  - b³

de lo que se puede concluir que para que una expresión algebraica es cubo perfecto de un binomio debe cumplir con las siguientes características:

a) Estar ordenado con respecto de una letra.

b) Que el primero y último término sean cubos perfectos.

c) Que el segundo término sea tres veces el cuadrado de la raíz cúbica del primer término multiplicada por la raíz cúbica del último término.

d) Que el tercer término sea tres veces la raíz cúbica del primer término multiplicada por el cuadrado de la raíz cúbica del último término.

e) Si los signos del resultado son todos positivos, el binomio será de la forma  (a + b)³, y si los signos van alternados (+, -, +, -) será de la forma  (a - b)³.

Ejemplo.

Factorizar:    27 – 27x + 9x² – x³

Veamos si esta expresión cumple  con las condiciones para que sea el cubo perfecto de un binomio:

Raíz cúbica de  27 =  3

Raíz cúbica de  x³ =  x

Segundo término  =  3 (3)²(x)  = 27x

Tercer término    =  3 (3) (x) ² =  9x²

Y como los signos vienen alternados, la expresión algebraica dada es el cubo perfecto de  (3 – x)³ es decir:

 27 – 27x + 9x² – x³   =  (3 – x)³

Ejemplo.

Factorizar:     125a³ + 150a²b + 60 ab² + 8b³

Raíz cúbica de  125a³  = 5a

Raíz cúbica de  8b³ =  2b

Segundo término  = 3 (5a)²(2b)  = 150a²b

Tercer término    =  3 (5a) (2b)²  = 60 ab²

Y como los signos son todos positivos, la expresión algebraica dada es el cubo perfecto de  (5a  + 2b)³ es decir:

125a³ + 150a²b + 60 ab² + 8b³   =  (5a  + 2b)³

5.2.9  Caso IX.  Suma o diferencia de cubos perfectos

Vimos en cocientes notables que:

a³ + b³  = (a + b) (a² – ab + b²)

a³ - b³  = (a - b) (a ² + ab + b²)

Estos dos enunciados se utilizan para Factorizar la suma o diferencia de un cubo perfecto.

Ejemplos:

1. Factorizar:      x³ - 27

Vemos que es de a forma    a³ - b³  = (a - b) (a² + ab + b²)

Luego:   raíz cúbica de    x³  =  x

              raíz cúbica de  27   =  3

Entonces:      x³ – 27  =  (x - 3) (x² + 3x + 3²)

                                   =  (x - 3) (x² + 3x + 9)

2.  Factorizar:       8x³ + y³

Vemos que es de la forma    a³ + b³  = (a + b) (a² - ab + b²)

Luego:    raíz cúbica de    8x³  =  2x

              Raíz cúbica de      y³  =  y

Entonces:   8x³ + y³ =  (2x + y) (4x² – 2xy + y²)

5.2.10  Caso X.  Suma o diferencia de dos potencias iguales

También se vio en los cocientes notables que:

a) aⁿ - bⁿ  dividido entre  a – b es siempre divisible, siendo n cualquier número entero, sea par o impar.

b) aⁿ - bⁿ  dividido entre  a + b es siempre divisible, si n  es un número entero  par.

c) aⁿ + bⁿ  dividido entre  a + b es siempre divisible, si n  es un número entero  impar.

d) aⁿ + bⁿ  dividido entre a + b  o   a – b  nunca es divisible, siendo n  un número par.

Ejemplos.

Factorizar: